Experiments in Certified Digital Audio Processing
Emilio J. Gallego Arias
(joint work with Pierre Jouvelot)
MINES ParisTech, PSL Research University, France
11 Avril 2016 - Specfun - Palaiseau
Real Time Signal Processing
$\cap$
Programming Language Theory
$\cap$
Theorem Proving
FEEVER ANR Project
Audio Objects
Recursive 2nd order Filter
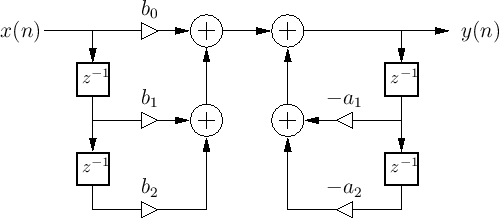
Image Credits: Julius Orion Smith III
Waveguide Resonator
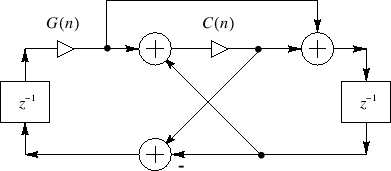
Image Credits: Julius Orion Smith III
Questions?
- Implementation ease?
- Composability?
- Mathematical Semantics?
- FP Semantics?
- PL Semantics!
- Domain practice.
- Frequency response.
- State Space.
- Optimization.
A Possible Roadmap
Julius Orion Smith III audio-focused book's series:
- Mathematics of the Discrete Fourier Transform (DFT) [Partially handled + missing inf. sum.]
- Introduction to Digital Filters [Focus of this talk]
- Physical Audio Signal Processing [Minor bits in this talk + missing ODE]
- Spectral Audio Signal Processing [Future work]
Main Points of the Series:
- Free mix of mathematics and a little computation.
- Linear algebra is pervasive.
- Proofs of uneven difficulty, not constructive-friendly.
Our View
Audio processing:
repeated linear algebra.
Audio programs:
finite approximation of the mathematics.
Topic of interest:
reconcile the algebraic and synchronous worlds.
Where to Look?
DSP & Theorem Proving
Isabelle/HOL[Akbarpour, Tahar et al.]
Focus on fixed systems, numerical issues.
Lucid, Velus[Boulmé, Auger, ...]
Safety Property, some work unpublished?
Kahn Networks[Paulin-Mohring]
Domain Theory point of view, setoid-rewriting based.
VeriDrone Project[Ricketts, Machela, Lerner, ...]
Work in progress, from LTL to Lyapunov!
FFT in Coq [Capretta]
Main successor of our current world view.
Likely more work that we are unaware of...
DSP & Programming Languages
Arrows/FRP [Elliot, Hughes, Hudak, Nilsson, ...]
Too abstract, not convenient for sample-based DSP view.
Synchronous Languages [Berry, Caspi, Halbwachs, Pouzet, ...]
Far from a "linear algebra" view, not particularly well suited
for DSP, (state of the art: [Guatto]'s PhD).
Data-intensive vs control-intensive require quite
different control techniques. [Berry, 2000]
DataFlow Languages [Lee, Thies, ...]
IMHO most successful approach so far, weak on formalization?
String Diagrams [Bonchi, Sobocinski, Zanasi]
Very interesting recent research, covers a limited subset of DSP.
Other Approaches
VOBLA, Ziria, Halide, Darkroom, Julia, Spiral, FeldSpar
Varying degrees of formal semantics.
A First Try: Mini-Faust & Coq
- Start from Faust [Orlarey 2002]: functional DSL for DSP based on arrow-like point-free combinators.
- Implement in Coq: step-indexing, math-comp.
- Define a (sample-based) logic for reasoning about this programs.
- Works nicely for easy examples; supports self-composition, etc...
Problems with the approach:
- Theorems in DSP not expressed in point-free combinators.
- PL methods awkward for DSP experts.
- Doesn't work so well for more complex examples.
Example: Filter Stability
In PL terms:
$$ \fjud{x \in [a,b]}{\mathsf{*(1-c) : + \sim *(c)}}{x \in [a,b]} $$
In DSP terms:
The impulse response decays to 0 as time goes to infinity.
High number of components make PL proof methods impractical.
What now? Wagner
Simple λ-calculus with feedback, variables carry a time index.
Types and Syntax:
Wagner: Operational Semantics
We use a big-step, time-indexed style. Every program reduces to a value at a given time step $n$. Equivalent to synchronous dataflow.
Examples: DF-I Filter

Note the overload of $x \cdot y$! The types of $a$ and $b$ will fix the op.
Examples: DF-II
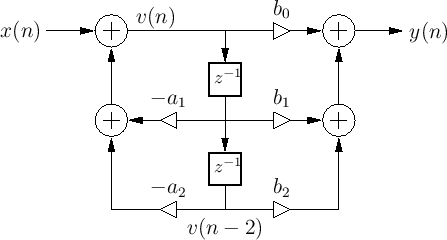
Compare with df1:
Examples: WaveGuide OSC

or without sugar:
Typing and Equational Theory
Typing is almost standard: we restrict pre to variables and use coeffect-inspired annotations to keep track of history-access. We also subtype rated streams to arrays:
We can recover the general pre as:
Application has to distinguish between positive and negative types to correctly propagate environment annotations. For this talk we use a restricted functional type.
Note: Work in coeffects, focusing, and duality is relevant and moslty subsumes our rules.
Now the fun starts
Lightweight embedding into Coq, use a mildy-typed syntax for a reduced subset (recall that: $ R ⇒ R ⇒ R ≈ R ⊗ R → R $):
Interpreting the Programs:
We want an easy embedding and "executable" embedding, our evaluation relation is not. Basically we are looking for something such as:
However, what should the value of:
Indeed, we need to equiq the environments with history, thus they become list of lists of values. A first try for the interpretation could be:
Step-Indexing
However it is not enough, as when interpreting λ we don't have enough history!
We must use a strong induction principle so the application rule can compute all previous values:
Many more refinements are possible!
Case Study I: Linearity
The first application is to study the set of linear Wagner programs, as a first step towards the theory for linear systems and in particular, the Z-transform.
Adding programs:
What should linearity mean for our programs? The proper definition involves something known as a logical relation:
The relation is simple but would also work at higher-types. If we restrict the syntax to linear programs, we every program satisfies the relation!
The proof proceeds first, by induction on the typing derivation, then by induction on the number of steps.
Case Study I: Linearity
What about multi-linearity?
Compare: $$ \begin{array}{l} λ x. Λ y . x \cdot y : R → S ⇒ T \\ Λ x. Λ y . x \cdot y : R ⇒ S ⇒ T \end{array} $$
Work in progress: Relate to the completeness theorem for signal dataflow! [Bonchi, Sobociński, Zanasi 2015/2016] [Baez]
Case Study II: Frequency Domain
Quick Review
- The frequency response of a filter = output for the impulse response.
- A filter is stable = its Frequency Response is summable.
- Stability is implied by the existence of the DTFT.
- The DFT approximates the DTFT.
- The DTFT is the evaluation of the Z-transform for the unit circle.
Crucial Prerrequisites:
- Previous linearity theorem.
- A notion of DFT in Coq.
Geometric Signal Theory
The DFT:
$$ X(\omega_k) = \ip{x^T, \omega_k} ~~\text{where}~~ \omega_k = \omega^{k*0},\ldots,\omega^{k*(N-1)} $$Most properties are an immediate consequency of matrix multiplication lemmas. Again life is easy here.
In matrix form:
Primitive roots:
The constructive algebraic numbers in mathcomp provides us with a primitive root of the unity such that $ω^N = 1$.
In an Ideal World...
... we'd have everything we need in our library.
- We are not so far from it.
- Took the definitions from classfun.v and proved:
Energy theorems are trivial corollaries. Quite compact development for now.
Transfer Functions
We want to relate programs to their frequency semantics; it is well known that:
$$ H(e^{jωT}) = \text{DTFT}_{ωT}(h) $$We'd like to relate programs to their transfer function:
Z-interpretation of programs
We tried to build an effective procedure, however it is difficult.
Current approach: Using a relation
Z-interpretation of programs
We can thus prove:
We show then that evalution of the impulse response DFT corresponds to the polynomial plus a residual based on the poles.
Stability is implied if the magnitude of all the poles is less than 1. This also implies the existence of the DTFT.
Implementation: The SSSM Abstract Machine
Open Topics
- Multirate processing: [quite a bit working]
- State Space analysis, control theory, MIMO systems
- Floating Point Interpretation.
- Schur-Cohn Stability Test
- Verification of transforms optimization. [Püschel]
- Computational Z-interpretation:
- Connection to more mainstream numerical approximation literature?
Conclusions
- Implementation in Ocaml with a core type system. Full type system still not fully settled, interesting desing space.
- Same for Coq formalization, theorems are working but more experience is needed to choose some implementation details (for instance, choice of environment representation
- Next logical step: COLA/OLA.
- We are particularly excited to see what the relation with SPIRAL could be.
- Numerical issues are pervasive in this domain, but trying to get there. Library for floating point aritmetic in progress.
- Missing an integrated library for true real and complex numbers, recent effort by PY and Assia? Should we port Coquelicot?
Thanks!
Thanks!


Context of the ANR project:
Practice of real time DSP still far from convenient.
Starting point, Faust:
- Faust [Orlarey 2002], a functional PL for audio programming.
- Abstracts away low-level complexity, efficient execution.
- A success, good number of users, high-interest topic. (CCRMA workshops, Kadenze course, etc...)
Faust's Future:
- Extend Faust to multirate processing.
- Reasoning about audio programs is not easy.
A note on streams.
The beggining of it all:
First exercise, port of Lucid paper to modern Coq/Ssreflect; // broken with coinductives! Dependent types not very scalable; decidability/extensionality of streams: bad.
Move to sequences!
"Inversion views", but better, wf_str is decidable now!
/